Below is an email I received from a sports bettor this week, with the subject line of “Northwestern’s Sportsmanship Saved Me.” A sophomore at Indiana University, this bettor endured the sweat of a lifetime this past Saturday with a nine-team college basketball/football parlay. For example, a 5-team round robin bet at most 4-ways would consist of 25 bets in total (5 4-team parlays, 10 3-team parlays, and 10 2-team parlays). This calculator determines the maximum win. Parlay Calculator. Our parlay calculator will combine up to 12 games and calculate your payout based on your bet amount and the odds for each game. Find out how much you'll win on any parlay. Betting Calculator Parlay Calculator Bet Slip. A parlay is a wager type in which multiple bets are linked together to create a greater payout. But since it’s treated as one big bet, every game in a parlay must win for the bet to win. If even one game loses, the parlay loses. Sportsbooks give you bigger and bigger payouts for adding more games to a parlay.
Most gamblers don’t care how a Parlay Calculator works.
But not you.
You are better than most!
On this page you’ll learn how a parlay calculator works and different strategies for improving your gambling skills. Here's the plan:
- How is a parlay calculated.
- Why should I care?
- What is a Parlay Bet?
- Parlay Odds Table.
- Getting Started with Parlay Tips
How is a Parlay Calculated?

Lets start with the math.
The parlay formula is straight forward. You multiply the wager amount along with the decimal odds for each team/fighter then subtract the wager amount.
UFC Parlay Calculation Formula
- Edson Barboza at 1.60
- Israel Adesanya at 2.90
- Max Holloway at 1.40
($100 * 1.6 * 2.9 * 1.4) - $100 = $550
For all of us in the US, it’s a bit more complicated because we don’t see decimal odds very often. So we first need to convert the money line odds to decimal odds then plug them into our parlay formula.
The money line-to-decimal formula is straightforward:
- Favorites - A negative value (-250) money line divide 100 by the number. 100/250 = .4
- Underdogs - A positive value (+180) money line divide the number by 100. 180/100 = 1.8
- Add 1 to the value for both favorites and underdogs.
- Plug these numbers into the parlay formula mentioned above.
Money Line Parlay Calculation Example
- Edson Barboza -165
- Israel Adesanya +190
- Max Holloway at -255
Steps 1 & 2.
- Edson Barboza 100/165 = .60
- Israel Adesanya +190/100 = 1.90
- Max Holloway at -100/255 = .40
Step 3 - Don't forget to add the 1.
- 1.6
- 2.9
- 1.4
Step 4 - Plug the numbers into the parlay calculator formula.
($100 * 1.6 * 2.9 * 1.4) - $100 = $550
Why Should I Care How the Parlay Calculator Works?
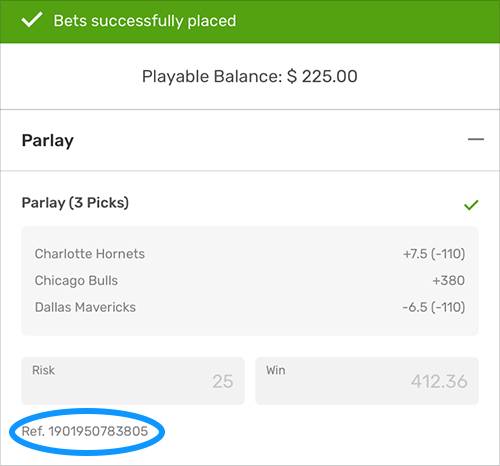
You should compare the results from this formula to what your sports book is paying to verify you’re getting the proper value on your wagers. If not, consider moving your business elsewhere.
An educated gambler is always a better gambler and with a thorough understanding of basic parlay principles you’ll soon spot profitable opportunities while recognizing common money pits.

A parlay, accumulator (or acca), combo bet or multi is a single bet that links together two or more individual wagers and is dependent on all of those wagers winning together. The benefit of the parlay is that there are much higher payoffs than placing each individual bet separately, since the difficulty of hitting all of them is much higher. If any of the bets in the parlay lose, the entire parlay loses. If any of the plays in the parlay ties, or 'pushes', the parlay reverts to a lower number of teams with the odds reducing accordingly.
Odds and payout[edit]
Parlay bets are paid out at odds higher than the typical single game bet, but still below the 'true' odds. For instance, a common 2-team NFL parlay based entirely on the spread generally has a payout of 2.6:1.[citation needed] In reality however, if one assumes that each single game bet is 50/50, the true payout should instead be 3:1 (10% expected value for the house). A house may average 20-30% profit on spread parlays compared to perhaps 4.5% profit on individual sports mix parlay bets.
Aside from 'spread' parlays, another way to parlay is to bet on two or more teams simply winning straight up. In order to calculate the payout of this parlay, one must multiply out the payout for all games. For example, if 3 teams are -385 favorites, a successful parlay on all 3 teams winning would pay out at a ratio of approximately 1/1. This is because (385/485)^3 is approximately 50%.
Money Line Parlay Odds Calculator
Examples[edit]
Typical payouts for up to 10 team parlay bet[edit]
The following is an example of a traditional Las Vegas Parlay Card at William Hill Sports Book, which shows the typical payouts for an up to 10 team parlay bet based on -1.10 prices (amount won is assuming $100 is bet)[citation needed]:
| Number | Odds | Amount won | Payout |
|---|---|---|---|
| 2 Team Parlay | 2.6 to 1 | $260 | $360 |
| 3 Team Parlay | 6 to 1 | $600 | $700 |
| 4 Team Parlay | 11 to 1 | $1,100 | $1,200 |
| 5 Team Parlay | 22 to 1 | $2,200 | $2,300 |
| 6 Team Parlay | 45 to 1 | $4,500 | $4,600 |
| 7 Team Parlay | 90 to 1 | $9,000 | $9,100 |
| 8 Team Parlay | 180 to 1 | $18,000 | $18,100 |
| 9 Team Parlay | 360 to 1 | $36,000 | $36,100 |
| 10 Team Parlay | 720 to 1 | $72,000 | $72,100 |
Profitability of parlays in sports betting[edit]
Many gamblers have mixed feelings as to whether or not parlays are a wise play. The best way to analyze if they are profitable in the long term is by calculating the expected value. The formula for expected value is: E[X] = x1p1 + x2p2 + x3p3…xkpk . Since the probability of all possible events will add up to 1 this can also be looked at as the weighted average of the event. The table below represents odds.[citation needed]
Column 1 = number of individual bets in the parlay
Column 2 = correct odds of winning with 50% chance of winning each individual bet
Column 3 = odds payout of parlay at the sportsbook
Column 4 = correct odds of winning parlay with 55% chance of winning each individual bet
10 Team Parlay Calculator
| Number of individual bets | Correct odds at 50% | Odds payout at sportsbook | Correct odds of winning parlay at 55% |
|---|---|---|---|
| 2 | 3 to 1 | 2.6 to 1 | 2.3 to 1 |
| 3 | 7 to 1 | 6 to 1 | 5.0 to 1 |
| 4 | 15 to 1 | 12 to 1 | 9.9 to 1 |
| 5 | 31 to 1 | 24 to 1 | 18.9 to 1 |
| 6 | 63 to 1 | 48 to 1 | 35.1 to 1 |
| 7 | 127 to 1 | 92 to 1 | 64.7 to 1 |
| 8 | 255 to 1 | 176 to 1 | 118.4 to 1 |
| 9 | 511 to 1 | 337 to 1 | 216.1 to 1 |
| 10 | 1,023 to 1 | 645 to 1 | 393.8 to 1 |
| 11 | 2,047 to 1 | 1,233 to 1 | 716.8 to 1 |
The table illustrates that if a 55% chance of winning each individual bet were achievable, parlays would be profitable in the long term. Compare the expected value you receive on an individual bet at a typical price of -110 with a 55% chance of winning: ((100/110+1)*.55)-1 = .05 (exactly 5 cents won for every dollar bet on average), multiplied by 11 = .55, to the expected return on the 11 game parlay ((1234/717.8)-1) = .719 (72 cents won for every dollar bet on average). In this case a parlay has a much higher expected value than individual bets with greatly increased variance in outcomes.